Alright, so I decided to finally try and get my head around this Ito’s Formula thing. Everyone in finance, or anyone touching stochastic calculus, seems to bring it up. Sounded fancy, and honestly, a bit intimidating. My math classes were a long time ago, you know?

Getting Started – Or Stumbling, Rather
So, I figured, how hard can it be? Famous last words. I cracked open a textbook – big mistake. It was like a wall of Greek letters and symbols I barely recognized. The `dWt` term, that Wiener process thing, was everywhere. And then they hit you with `(dWt)^2 = dt`. My brain just slammed the brakes. How does squaring a tiny random bit give you a tiny deterministic bit of time? Made no sense to me. Regular calculus taught me to ignore tiny squared things, they just vanish. This was different.
I spent a good few evenings just staring at that equation, trying to make it click. It felt like trying to understand a magic trick where you know there’s a logical explanation, but it’s hidden just out of sight.
The “Let’s Try Something Simpler” Phase
Okay, textbooks weren’t cutting it for me initially. Too dense. So, I thought, let’s look for simpler explanations. Watched a few online lectures. Some were okay, but many quickly ramped up to a level that left me behind again. They’d start with a simple idea and then, boom, five minutes later, we’re deep in measure theory or something.
My next approach was to try and work through it with a really basic function. Like, what if `f(W_t) = W_t^2`? I thought I could just use the good old Taylor expansion. So, I tried:
`df = f(W_{t+dt}) – f(W_t)`

And I started expanding `(W_t + dW_t)^2`.
You get `W_t^2 + 2W_t dW_t + (dW_t)^2 – W_t^2`.
Which simplifies to `2W_t dW_t + (dW_t)^2`.
And there it was again, that pesky `(dW_t)^2`. In normal calculus, if `dx` is small, `(dx)^2` is super small, you toss it. But here, with Ito, you can’t. That was the hurdle. This was the part that really got me stuck for a while.

Slowly Seeing the Light (Maybe?)
It wasn’t a sudden “eureka!” moment. It was more like a slow dawning. The thing is, `dWt` isn’t just a small number; it’s a random variable with a certain variance. And that variance over a small time `dt` is actually `dt`. So, `(dWt)^2` isn’t negligible; it behaves like `dt` on average. This felt super counter-intuitive at first. It’s like the randomness has its own rules that bend what you expect from regular calculus.
So, the full Ito’s formula for a function `f(t, X_t)`:
`df = (∂f/∂t)dt + (∂f/∂X)dX_t + (1/2)(∂^2f/∂X^2)(dX_t)^2`
And if `X_t` follows something like `dX_t = a dt + b dW_t`, then `(dX_t)^2` becomes `b^2 (dW_t)^2 = b^2 dt`. That extra term, the `(1/2)(∂^2f/∂X^2)b^2 dt`, is the “Ito term.” That’s the correction you need because you’re dealing with these jumpy random processes.
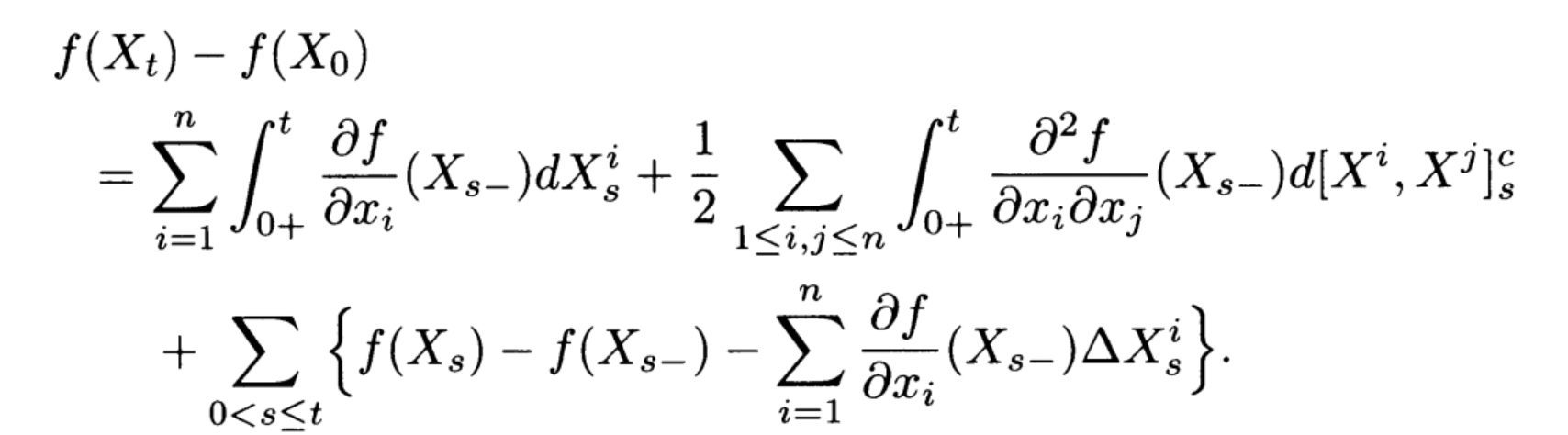
I had to write this out multiple times, for different simple functions, before it started to feel even slightly natural. It’s one of those things where you kind of have to just accept the rule `(dWt)^2 = dt` and see where it leads you.
What I Got Out Of It
So, did I become an Ito’s Formula guru? Definitely not. Not by a long shot. But I feel like I climbed a small hill. I can now look at a formula that uses it, like in the Black-Scholes option pricing model, and not be completely bewildered by that extra term. I have a sense of why it’s there.
It was a bit of a slog, not gonna lie. There were moments I just wanted to close the book and say “this isn’t for me.” But pushing through, even to get a basic grasp, was kind of satisfying. It’s a reminder that some concepts in math, especially those dealing with randomness, just don’t map nicely to our everyday intuition. You have to build a new intuition for them.
My main takeaways were:
- Don’t assume random processes behave like smooth functions. They don’t.
- The `(dWt)^2 = dt` rule is weird but crucial. You just have to roll with it.
- Working through simple examples by hand, even if it feels silly, helps way more than just reading theory.
So yeah, that was my little adventure into Ito’s Formula. Still feels a bit like looking at a complex machine, but at least now I think I know what a couple of the levers do. It’s a process, right?
