Okay, so I sat down this morning, coffee steaming beside my notebook, thinking I’d tackle something basic. You know, the kind of thing people might get stuck on. Then it hit me – fractions dividing into whole numbers. I remembered seeing folks trip up on questions like “What is 2 divided by 1/4?” all the time online. Seems straightforward, right? But I know from experience that fraction division can be a real head-scratcher if you’re rusty.
Starting Simple
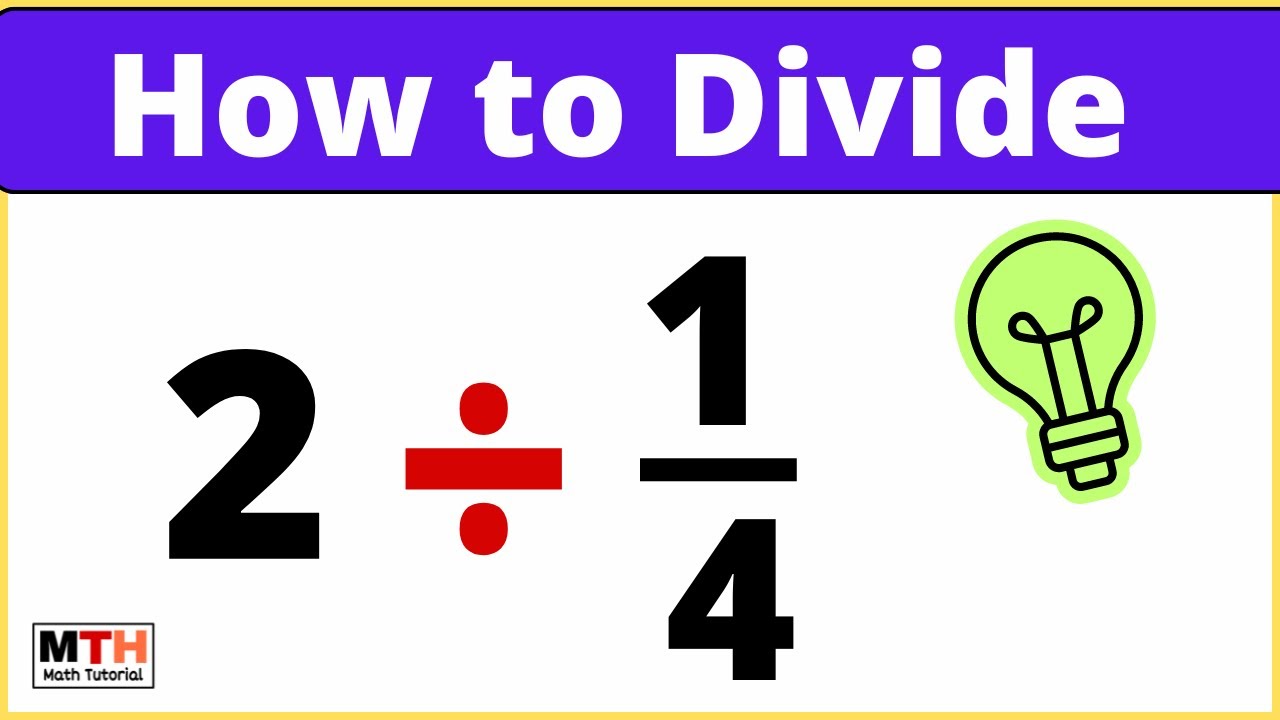
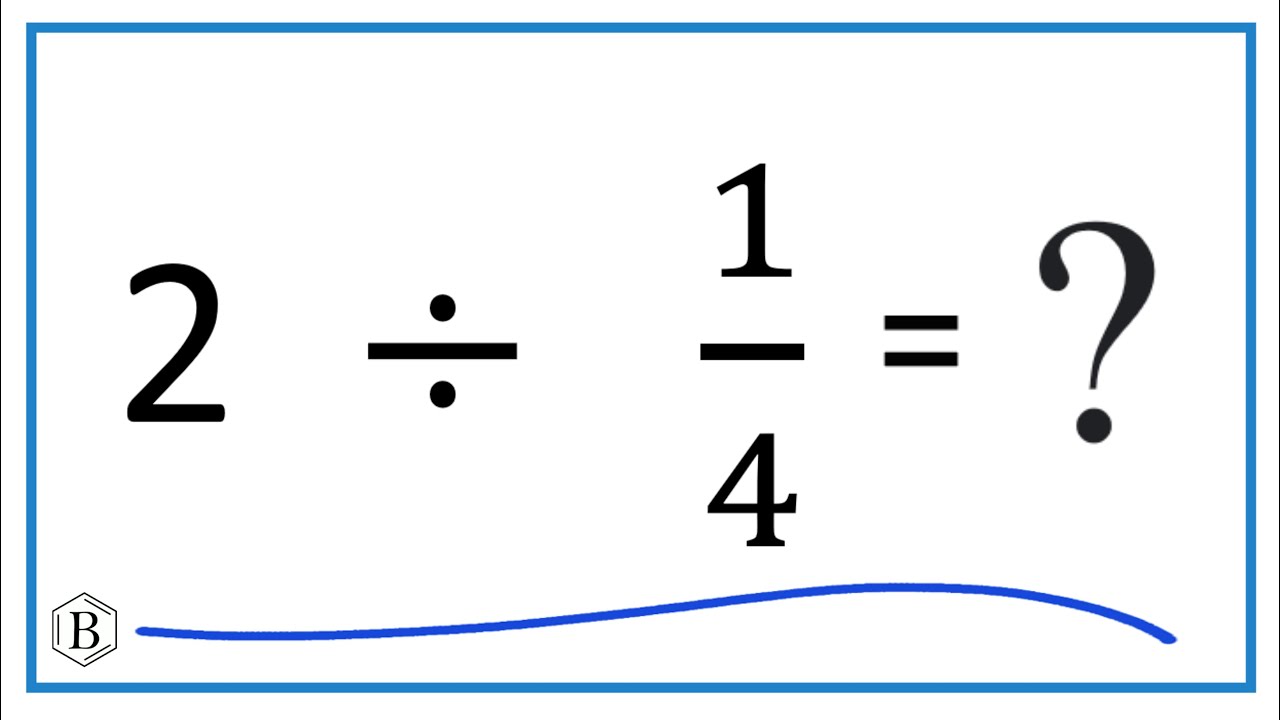
I grabbed my pencil. Step one: I wrote down exactly what we’ve got: 2 ÷ (1/4). I looked at that little divided-by sign. I thought, “Okay, dividing by a fraction… what does that actually mean?”
It’s like asking: How many pieces of size 1/4 can I fit into the whole number 2? Picture it like this: You’ve got two whole pizzas. If you need to cut each pizza into pieces that are 1/4 of a pizza each… well, how many slices do you get total? That clicked for me.
Working it Out
This is where the old trick comes in handy. Instead of banging my head against division, I remembered: Dividing by a fraction is the same as multiplying by its upside-down version. The reciprocal, they call it.
Here’s what I did:
- First, I kept the first number as is: 2.
- Then, I looked at the divisor: 1/4.
- Next, I flipped that fraction upside-down! Turned 1/4 into 4/1. Simple flip.
- Then, I swapped that pesky ÷ sign for a nice, friendly × sign. So now I had: 2 × (4/1).
Finishing the Math
Okay, this looked much easier. 2 × (4/1) is just multiplication.
- Multiplying the whole number 2 by that fraction. 2 is the same as 2/1, so I wrote it as (2/1) × (4/1).
- Now, multiplying fractions is a breeze. Multiply the tops: 2 × 4 = 8.
- Multiply the bottoms: 1 × 1 = 1.
- So, 8/1, which is just 8.
The Answer
So, 2 ÷ (1/4) = 8. It made perfect sense thinking back to those pizzas. Two whole pizzas, each cut into quarters? Each pizza gives you 4 slices, so two pizzas give you 8 slices. Fits perfectly!
Sometimes it’s easy to forget that little trick of flipping the fraction and multiplying. But man, once you remember it, problems like these become super simple. That’s how I walked myself through it again today – good to refresh the basics!
